The three guys in the painting below are all depictions of King Charles I, painted from different viewpoints by Anthonis van Dyck in 1636. In the middle we see a frontal view (“en face”), on the left a side view (“en profile”), and the most intriguing is the one on the right: the three-quarter view (“en trois quarts”). So here is the question that has bugged me for some time. Why is it called three-quarter, or 3/4? Three quarters of what?
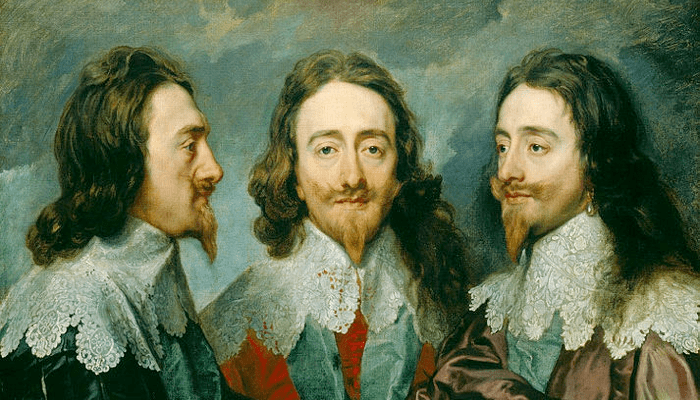
I have taken several actions to get an answer. Of course I browsed the web extensively. And trust me, I know how to find things. I have asked the artists in my family who have taken drawing classes at professional academies. All the answers came down to this: if the three-quarter view is 3/4 then the other two views must be 2/4 and 4/4. But there was no consensus on whether 2/4 corresponds to the frontal view or the side view. And no one could answer my question; which view is 1/4 or 0/4 in this line of reasoning? Views of the back of the head?
My hypothesis is this. The 3/4 refers to the proportion of the width and height of the head as it is painted on the canvas. In the drawing manuals I consulted, they set the height of the head as the standard equal to 1. The rest of the body is expressed as “number of heads” or “fraction of head height”. For example, the average person is 7 1/2 heads tall. I also found rules for drawing the head in frontal view with proportion 2/3 = 0.67 and from the side with proportion 7/8 = 0.88. Nowhere did I find an explicit mention of 3/4 = 0.75 for the “three-quarter” view.

> You can sign up for my newsletter here.
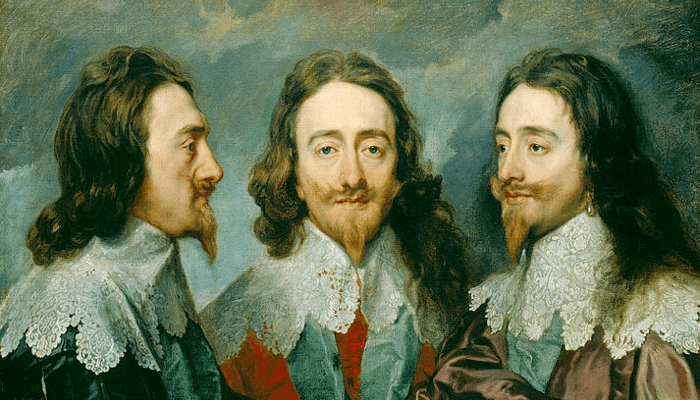
I think it come form you devind 0-90 degree of the head to 4 part so itgonna be 1/4 = 0-22.5 degree 2/4 = 22.5 – 45 degree 3/4 is 45-67.5 degree and 4/4 is 67.5-90 degree
@Paul @Veysi
I think Daniel had the right interpretation. Let me try to make it as clear as I possibly can.
Let’s start by assuming that the face covers about half of the head. If the nose points at you, you can see the whole face, a _full_ face in frontal view. Now consider the case that the head can rotate around the vertical; this is what happens when you shake “no”. If the nose points all the way to the left, or all the way to the right, you see the side of the head and _half_ of the face is visible. The view exactly in between the “side”=1/2 and the “front”=1 is the orientation of the head that we are interested in. In that case _3/4_ of the face is visible. So “3/4 view” = 3/4 of the face is in view.
In visuals (drawning, painting, video, photo…) I think it is about the angle between frontal view and side view (left or right). Frontal could be 0/4 or 1/4, side is always 4/4. So the face in the painting above is on the 3/4th from the frontal.
My intuition says for two reasons why the frontal should be 1/4:
– from 0/4 (frontal) to 4/4 (side) the four parts are too small to make a good difference for our eyes. We see the difference better in three parts from 1/4 (frontal) to 4/4 (side). That visually makes a good difference in the drawnings / paintings in the period before the renaissance, which are usually flat.
– when we drawn and divide a face into four parts by horizontal and vertical lines, we see it consists of four parts. So we see only the 1st part (1/4) to the 4th part (4/4). Visually and mathematically there is no 0 part (0/4).
I hope I explain it well.
My understanding is that 3/4 refers to the approximate portion of the _face_ that is visible. 4/4 would be face view and 2/4 would be side view.
BTW, 3/4 portraits go back much further than the Renaissance:
https://en.wikipedia.org/wiki/Niobid_Painter
[changed the link to a Wikipedia article – Stijn]
That makes a lot of sense: the fraction of the face that is visible. Thank you, Daniel! So strange that I have never found a description of it in these terms.
Also thanks for the 3/4 view example from antiquity. I was not aware of it.
Refined theory: 0/4 would be looking in the same direction as the subject; 1/4 would be looking at his or her ear if human; 2/4 would be a side view; 4/4 would be directly facing the subject. The engineer in me wants to liken this to the use of radians to specify an angle.
The most common angular units are of course “degrees” and “radians”. If you define the nose in the direction of the viewer as 0, you would get something like 45 degrees or π/4. Wherever you define the origin, you would get numbers between 0 – 360 and 0 – 2π respectively. The 3/4 does not seem to refer to any obvious angle.
You suggest something similar to a “turn”, usually defined as equal to 1 for a full rotation. So, our “3/4 view” would be at 1/8.
I am guessing that the key to this riddle will be somewhere in the visual arts literature that emerged in the Renaissance when the first 3/4 view portraits were painted.
Disagreement about sign (smile) I believe that the king’s portraits are: 2/4 of a radian to the right; 4/4 of a radian; and 3/4 of a radian to the left, where 0/4 is looking the same direction as the subject is looking.
I believe that 3/4 refers to the point of view – rotated 3/4 of the way from a side view towards a front view. But darn it, I can find my old mechanical drawing book for verification. YouTube has videos about drawing faces and cars from that point of view.